【概要】
このドキュメントでは、モーメントの計算により、複葉機説の方が垂直尾翼説よりも妥当であることを示しました。
結論から言えば、垂直尾翼説の場合、モーメントのバランスを考慮すると、翼面荷重が複葉機説の1.5倍も高くなるんです。ただでさえ重くて揚力不足気味なのに1.5倍も荷重を増やすのは飛行生物としてどうなんだろう。
ああ、それと複葉機説の場合は、足の翼にに後退角をつけるか、あるいは尾羽を外に広げるなどして尾の面積を19%広げるとより幸せになれるかもしれません。
【本論】
(1)翼面積の比率を求める
厳密には翼型や迎え角などの条件により揚力は変化しますが、本ドキュメントでは揚力は翼面積に比例すると仮定して話を進めます。まずは各翼の翼面積の比率を求めてみましょう。(※)
筆者は翼面積の比率を求める方法として、下記の手順を行ないました。
(1)元の図版を切り出す
(2)各翼をペイントツールで青で塗りつぶす
(3)このためだけにVBで30分ほどかけて作った自作プログラムで(※)、画像内の青いピクセルの数を数える
※ 『なぜ実際の面積でないのか』という疑問があるかもしれませんが、モーメントと言うのはバランスの問題=比率の問題なので、実際の面積である必要は無いのです。
※ 実行ファイルとソースをここに置いときますね。(Windows用です。)BluePointCount.lzh
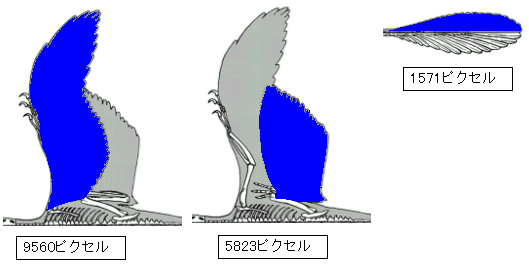
そこで、青いピクセルを数えてみた結果が
上図の結果より、各翼面積の比率は、
腕の翼:足の翼:尾の翼 = 9560:5823:1571
≒ 100:61:16
となります。
(2)複葉機説でのモーメントを計算してみる
それでは複葉機説で、グイに働くモーメントを作図してみますか。
図版を基に、重心点からの距離をピクセル単位を測ってみると、こうなります。
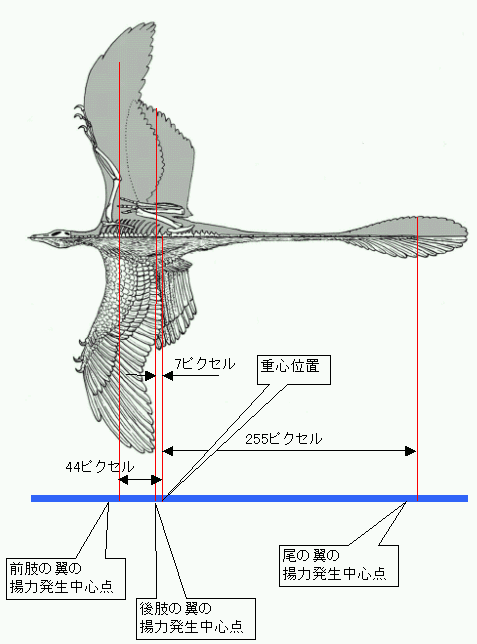
さて、前半の揚力の発生するモーメントと後半の揚力が発生するモーメントがつりあいが取れていることが必要です。
重心位置から前半にあるのは、腕の翼、足の翼。後半にあるのは、尾の翼ですね。
| モーメントの内訳 | |
| 前半のモーメント | [腕の翼の重心からの距離]*[腕の翼の発生する揚力] +[足の翼の重心からの距離]*[足の翼の発生する揚力] |
| 後半のモーメント | [尾の翼の重心からの距離]*[尾の翼の発生する揚力] |
それでは、図1、図2から求めた値をこの式に代入してみましょう。
| モーメントの内訳 | |
| 前半のモーメント | 44 * 100 + 7 * 61 = 4827 |
| 後半のモーメント | 255 * 16 = 4080 |
前半の揚力がいくぶん大きめです。
これを解消するためには尾羽の面積が後どのくらい必要でしょうか。
4827 = 255 * X
X = 18.92941
つまり尾羽がもう少し広がり気味で、尾羽の翼面積が19%増えていた場合、あるいはいくらか迎え角を増やして揚力を19%増大させた場合、バランスが取れることになります。
ここでちょっと視点を変えて、足の翼に後退角がついていた可能性を考えましょう。
足の羽に後退角がつくことで、足の羽の揚力発生中心点が、重心の6ピクセル後ろに移動したとします。
その場合は、足の揚力が後半のモーメントに含まれますからこうなります。
| モーメントの内訳 | |
| 前半のモーメント | [腕の翼の重心からの距離]*[腕の翼の発生する揚力] |
| 後半のモーメント | [尾の翼の重心からの距離]*[尾の翼の発生する揚力] +[足の翼の重心からの距離]*[足の翼の発生する揚力] |
| モーメントの内訳 | |
| 前半のモーメント | 44 * 100 = 4400 |
| 後半のモーメント | 255 * 16 + 6 * 61 = 4446 |
この結果から、ある程度の後退角を想定することでもバランスが取れることが分かります。
(3)それなら垂直尾翼説はどうなのか?
基の図版を切り張りして、垂直尾翼説の図版を作ってみました。コラ職人か俺は。
そのまま反転したり回転したりして作ったので、足の骨の長さとかは変えていません。
そしてできあがったのが図3です。
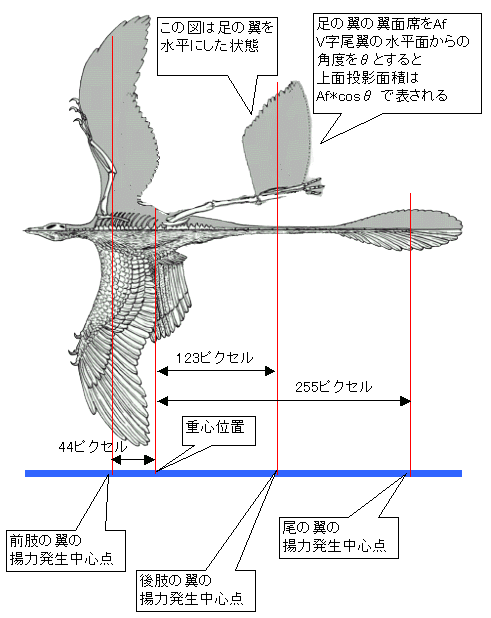
さて、ここで注意するべきは、足の翼がV字型の尾翼であるということです。 足の翼の翼面積をAf、足の翼の水平面からの角度をθとすると、上面から投影した翼面積は、下記の式で表されます。
Af * cosθ
つまり、翼が『垂直尾翼』に近づくほど(θが90°に近づくほど)上面から投影される翼面積は少なくなるわけです。
| モーメントの内訳 | |
| 前半のモーメント | [腕の翼の重心からの距離]*[腕の翼の発生する揚力] |
| 後半のモーメント | [尾の翼の重心からの距離]*[尾の翼の発生する揚力] +[足の翼の重心からの距離]*[足の翼の発生する揚力]*[Cosθ] |
それでは、足の翼の傾きを変えながらモーメントを比較してみますね。
| θ=0°(水平) | θ=30° | θ=45° | θ=60° | θ=90°(垂直) | |
| 前半のモーメント: | 4400 | 4400 | 4400 | 4400 | 4400 |
| 後半のモーメント: | 11583 | 10578 | 9385 | 7831 | 4080 |
この復元形態では、足の翼がほぼ完全に垂直に成らない限り、モーメントの帳尻が合わないことが分かります。
帳尻は合っているのだから別にいいだろうって?
垂直だともはや揚力を生まないんです。つまりこういうことになります。
| 翼面積の内訳 | 計算値 | |
| 複葉機説 | [腕の翼]+[足の翼]+[尾の翼] | 100+61+16=177 |
| V字尾翼説 | [腕の翼]+[尾の翼] | 100+16=116 |
つまり、足の翼が揚力を生まないため(もし揚力を生んだら前転します)、翼面荷重が177/116で5割増で高くなるわけです。
垂直尾翼としての効率も、モーメントアームが尾より短いのであまり良いとはいえません。むしろ尾羽を前方から見てV字型になるよう配置した方が良い結果が得られそうですね。
要するに、V字尾翼説は飛行体として明らかに複葉機説に劣る復元なのです。